학교 수업에서 진행한 머신러닝 강의 복습 및 리뷰. 우선 딥러닝의 성능 비교를 위해서 회귀 모형을 만들고, 깊이를 추가해 나가면서 그에 따른 성능(mse, loss)을 비교해 보겠다.
1. 회귀 모형
성능의 비교를 위해서 우선 간단한 회귀 모형을 작성한다. 추가로, 분석에 사용할 데이터 셋도 임의로 작성한다.
# 0. 사용할 패키지 불러오기
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import mean_squared_error
import random
import tensorflow as tf
import os
# 난수 고정
np.random.seed(42)
random.seed(42)
tf.random.set_seed(42)
os.environ['TF_DETERMINISTIC_OPS'] = '1'
# 1. 데이터셋 생성하기
x_train = np.random.random((1000, 1))
y_train = x_train * 2 + np.random.random((1000, 1)) / 3.0 # Y = 2X + ~(error값)
x_test = np.random.random((100, 1))
y_test = x_test * 2 + np.random.random((100, 1)) / 3.0
훈련 데이터를 Y = 2X + (오차값)의 형태로 생성한 이유는 딥러닝 모델을 포함한 회귀 모델이 명확한 선형 관계를 가진 데이터에서 얼마나 잘 학습하고 예측하는지를 평가하기 위함이다. + 노이즈(error값)으로 무작위성 추가.
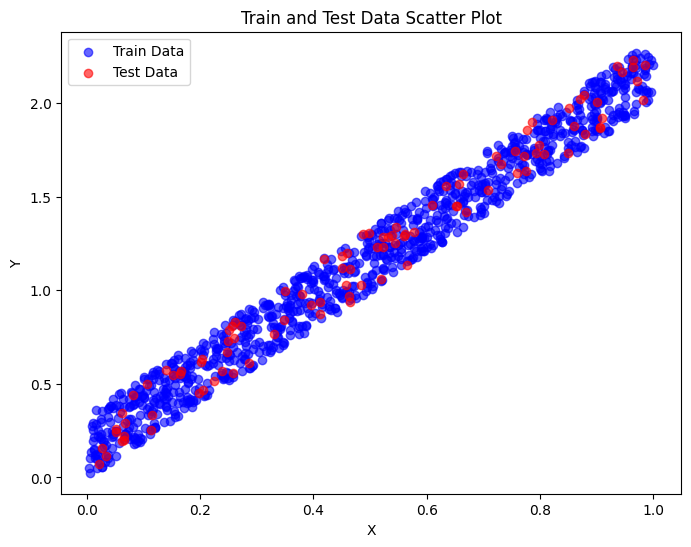
샘플 데이터가 선형이라서 선형 회귀가 높을 것으로 예상된다. -> 딥러닝 학습이 선형 회귀와 유사하면 성공!
x_train = x_train.reshape(1000,)
y_train = y_train.reshape(1000,)
x_test = x_test.reshape(100,)
y_test = y_test.reshape(100,)
x_train.shape
x_train
선형 회귀를 진행 하기 위해 1차원으로 데이터 형식을 바꿔준다. ( p.cov, np.var, np.mean 은 1차원 데이터를 받음, 2차원으로 회귀 시 추가 코드 필요)
# 2. 모델 구성하기 (회귀식의 추정)
w = np.cov(x_train, y_train, bias=False)[0,1] / np.var(x_train)
b = np.average(y_train) - w * np.average(x_train)
print (w, b) # y = b + wx
회귀 계수 (기울기, 가중치): 2.011783420867384 절편: 0.1632288690923035
Y=2.0117X+0.1632로 회귀식을 쓸 수 있다. 데이터를 생성할 때처럼 2와 가까운 기울기가 나타난다.
# 3. 모델 평가하기
y_predict = w * x_test + b
mse = mean_squared_error(y_test, y_predict)
print('mse : ' + str(mse))
평균 제곱 오차 (MSE): 0.00858277851953264
실제 값과 예측값 사이의 평균제곱오차 값이다. 낮을 수록 예측을 잘한단 뜻인데, 0.01로 좋은 성능을 보여준다. 그렇다면, 딥러닝을 어떤 성능을 보여줄 것 인가?
2. 딥러닝의 경우
# 0. 사용할 패키지 불러오기
import numpy as np
from keras.models import Sequential
from keras.layers import Dense
import random
# 2. 모델 구성하기
model = Sequential()
model.add(Dense(1, input_dim=1)
# 3. 모델 학습과정 설정하기
model.compile(optimizer='sgd', loss='mse')
model.summary()
Sequential()을 사용하여 모델을 초기화한후, Dense 레이어를 추가한다.
- units=1: 출력 뉴런의 수를 1로 설정
- input_dim=1: 입력 특성의 수를 1로 설정
- activation='relu': 활성화 함수로 ReLU를 사용 - 범주형일 경우 출력을 시그모이드로 사용하면 됨
- optimizer='sgd': 확률적 경사 하강법(SGD)을 옵티마이저로 사용
- loss='mse': 손실 함수로 평균 제곱 오차(MSE)를 사용
간단하게 나타내 보자면, X1 -(가중치 w)-> Y1 의 형태이다. 두 레이어 사이의 파라미터 개수는 (이전 레이어 길이 + 현재 필터 넓이)*이전 필터 크기 이다. 그러니까 (1+1)*1 의 형태로 나타낼 수 있으며 2개의 파라미터 개수를 구할 수있다. 요약 본으로 정답을 확인해본다.
Model: "sequential"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ dense (Dense) │ (None, 1) │ 2 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘
Total params: 2 (8.00 B)
Trainable params: 2 (8.00 B)
Non-trainable params: 0 (0.00 B)
이제 모델을 학습시켜 보겠다.
# 4. 모델 학습시키기
hist = model.fit(x_train, y_train, epochs=50, batch_size=64) # epochs은 몇개씩 짜를지,
w2, b2 = model.get_weights()
print (w2, b2)
해당 과정시 각 Epoch마다 손실 함수(loss)값이 출력되는데 손실 값이 감소하거나 안정화되면 모델이 수렴하고 있음을 나타낸다.
이때 epochs란, 전체 데이터셋을 모델이 완전히 한 번 학습하는 주기를 뜻한다. 현재 50으로 설정되있으니, 전체 데이터셋을 50번 반복하여 학습한다. 너무 많은 epoch 설정은 과적합을, 너무 작으면 충분히 학습되지 않을 수 있음을 유의하자.
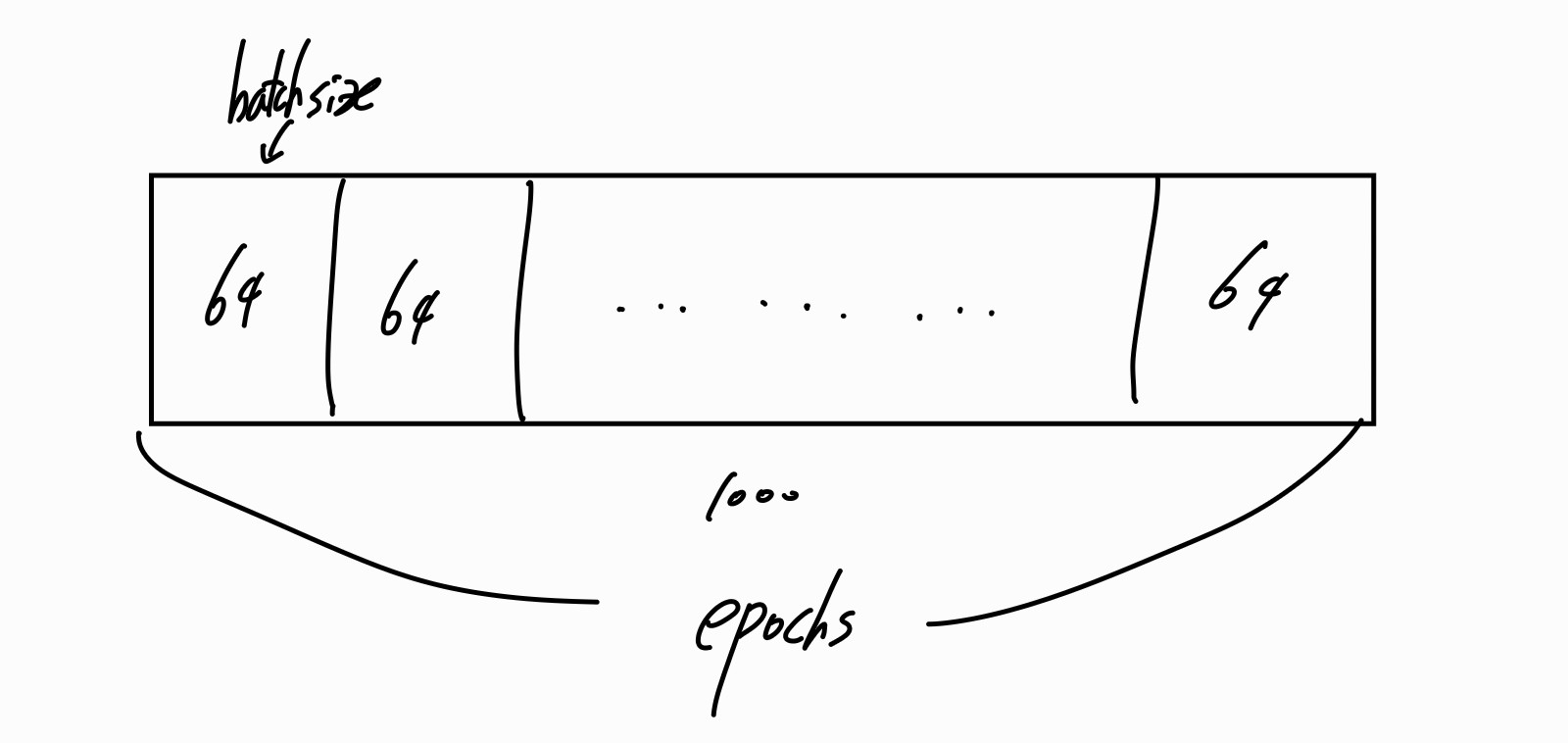
이때 한번 실행하는 데이터 개수를 batch size, 그럼 1000개의 데이터가 있으니까 1000/64를 해서 16의 배치를 가진다. 실행 결과를 보면 쉽게 이해가능하다. 이때 loss값이 줄어들지 않고 들쭉날쭉한 것을 보아 모델이 제대로 학습되지 않음을 알 수 있다.
배치 크기도 설정에 장단점이 있는데, 너무 작게 잡으면 학습이 세밀하게 이루어지고 메모리 사용량이 작으나, 너무 오래걸리고 노이즈에 민감하게 반응할 수 있다(과적합 발생 가능). 너무 크면 빠른 속도와 많은 샘플을 사용해 안정적이나, 메모리 사용이 늘고 과소적합이 발생가능하다.
Epoch 1/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 1s 11ms/step - loss: 0.3022
Epoch 2/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step - loss: 0.1533
Epoch 3/50
(생략)
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step - loss: 0.0136
Epoch 48/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step - loss: 0.0134
Epoch 49/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step - loss: 0.0133
Epoch 50/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step - loss: 0.0131
[[1.8283669]] [0.25974143]
Y=1.830905⋅X+0.25841138의 식을 가진다고 볼 수 있다.
# 5. 학습과정 살펴보기
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(hist.history['loss'])
plt.ylim(0.0, 1.5)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train'], loc='upper left')
plt.show()
# 6. 모델 평가하기
loss1 = model.evaluate(x_test, y_test, batch_size=32)
print('loss : ' + str(loss1))
일때 mse값으로 loss : 0.011221873573958874를 가진다. 해당 딥러닝 모델은 은닉층도 없고, 활성함수 설정도 하지 않은 상태이다.
# 2. 모델 구성하기(은닉층 1개 포함)
model = Sequential()
model.add(Dense(64, input_dim=1, activation='relu'))
model.add(Dense(1))
# 3. 모델 학습과정 설정하기
model.compile(optimizer='rmsprop', loss='mse')
model.summary()
이번에는 은닉층, hidden layer를 하나 추가 해보겠다. model.add(Dense(64, input_dim=1, activation='relu')) 부분이 추가된 은닉층이며, 64개의 노드를 가진다. 1개의 차원, 활성함수는 relu를 사용하여 비선형 변환을 수행, 복잡한 패턴을 학습하도록 한다.
model.add(Dense(1))는 출력층이다. 뉴런의 개수가 1개이다. 파라미터 개수를 구해보자면, (1+1)*64 + (64+1)*1 이므로 128 + 65 = 193개의 파라미터수를 가진다.
Model: "sequential_10"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ dense_19 (Dense) │ (None, 64) │ 128 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_20 (Dense) │ (None, 1) │ 65 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘
Total params: 193 (772.00 B)
Trainable params: 193 (772.00 B)
Non-trainable params: 0 (0.00 B)
학습을 시켜보면, 코드와 결과는 다음과 같다.
# 4. 모델 학습시키기
hist = model.fit(x_train, y_train, epochs=50, batch_size=64)
# 5. 학습과정 살펴보기
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(hist.history['loss'])
plt.ylim(0.0, 1.5)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train'], loc='upper left')
plt.show()
# 6. 모델 평가하기
loss2 = model.evaluate(x_test, y_test, batch_size=32)
print('loss : ' + str(loss2))
'''Epoch 1/50
Epoch 1/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 1s 17ms/step - loss: 1.6683
Epoch 2/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 1.1339
Epoch 3/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.7986
Epoch 4/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.5357
...
Epoch 16/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0099
Epoch 17/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0098
Epoch 18/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0098
Epoch 19/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step - loss: 0.0098
loss : 0.008531514555215836'''
epoch 가 수행됨에 따라 훈련 손실 값이 감소하여 Epoch 17 이후로 0.0098 수준에서 수렴하게 된다. 0.0085~ 부분은 테스트 손실 값(mse)이다.

손실 값은 초기에 급격히 감소한후, 일정 수준에서 수렴하는 형태를 보인다. 처음 1.6에서 점점 줄어들어 0.0098까지 수렴한다.
그럼 동일한 은닉층을 하나 더 만들면 어떨까?
# 2. 모델 구성하기(은닉층 2개 포함)
model = Sequential()
model.add(Dense(64, input_dim=1, activation='relu'))
model.add(Dense(64, activation='relu')) # relu로 비선형변환
model.add(Dense(1))
# 3. 모델 학습과정 설정하기
model.compile(optimizer='sgd', loss='mse')
model.summary()
'''Model: "sequential_5"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ dense_9 (Dense) │ (None, 64) │ 128 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_10 (Dense) │ (None, 64) │ 4,160 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_11 (Dense) │ (None, 1) │ 65 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘
Total params: 4,353 (17.00 KB)
Trainable params: 4,353 (17.00 KB)
Non-trainable params: 0 (0.00 B)'''
은닉층을 하나더 추가하였다. 이전같은 첫번째 레이어를 가지며 (128개의 파라미터), 2번째 Dense 레이어는 입력 차원이 64, 출력 차원이 64이기에 (64+1)*64 =4160이다. 출력 차원이 64개의 파라미터를 가지니, 총 4,353개의 파라미터를 가진다!
각층을 정리하면 다음과 같다.
a. 은닉층 1 (dense_9)
- 64개의 뉴런을 포함한 은닉층으로, 입력 차원은 1이며 ReLU 활성화 함수를 사용해 비선형 변환을 수행.
b. 은닉층 2 (dense_10)
- 또 다른 64개의 뉴런을 포함하며, 이전 은닉층의 출력(64 차원)을 입력으로 받음.
- ReLU 활성화 함수를 사용해 추가적인 비선형 변환을 수행.
c. 출력층 (dense_11)
- 출력 뉴런 1개를 포함하며, 최종 예측 값을 반환.
- 활성화 함수가 지정되지 않았으므로, 기본적으로 선형 활성화 함수가 사용됨.
이제 마지막으로 모델을 학습 시키고 평가해보자.
# 4. 모델 학습시키기
hist = model.fit(x_train, y_train, epochs=50, batch_size=64)
# 5. 학습과정 살펴보기
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(hist.history['loss'])
plt.ylim(0.0, 1.5)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train'], loc='upper left')
plt.show()
# 6. 모델 평가하기
loss3 = model.evaluate(x_test, y_test, batch_size=32)
print('loss : ' + str(loss3))
'''Epoch 1/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 1s 28ms/step - loss: 0.9047
Epoch 2/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - loss: 0.1672
Epoch 3/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0974
Epoch 4/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: 0.0793
(생략)
Epoch 38/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0099
Epoch 39/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0098
Epoch 40/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step - loss: 0.0098
Epoch 41/50
16/16 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step - loss: 0.0098 ..
loss : 0.008721329271793365'''
점차 안정되가기 시작하더니 39번째에 이르러서 0.098로 수렴하였다. 이때 더 낮아지지 않는 이유는 데이터의 노이즈(오차 값)의 수준 때문으로 완전히 제거할 수 없기 때문이다. 테스트 손실 값이 더 낮을 걸 볼때 일반화 성능이 높게 나타난다고 볼 수 있다.
정리하자면 다음과 같다.
print('mse : ' + str(mse)) # 회귀 모형
print('loss1 : ' + str(loss1)) #은닉 X
print('loss2 : ' + str(loss2)) #은닉 1개
print('loss3 : ' + str(loss3)) # 은닉층 2개
'''mse : 0.00858277851953264
loss1 : 0.012480237521231174
loss2 : 0.008531514555215836
loss3 : 0.008721329271793365'''
은닉층을 적절히 사용하니 선형회귀와 비슷한 결과가 도출 되었다. 그리고 너무 복잡한 모형은 오히려 좋은 성능을 보장 하지 않는다는 것도 알 수 있다.
'머신러닝' 카테고리의 다른 글
| 지도학습 - 주택 가격 회귀 예측모형 / 전처리 + 회귀모형 + KNN (0) | 2024.11.25 |
|---|---|
| 지도학습 - 대출 승인 결과 분류 예측모형 / 앙상블 (1) | 2024.11.23 |
| 지도학습 - 대출 승인 결과 분류 예측모형 / Tree,SVM (0) | 2024.11.14 |
| 지도학습 - 대출 승인 결과 분류 예측모형 / 전처리, 로지스틱 회귀모형, KNN (0) | 2024.11.13 |



