본문 바로가기
머신러닝

지도학습 - 주택 가격 회귀 예측모형 / 전처리 + 회귀모형 + KNN

by Seungyoon1786 2024. 11. 25.

이전에 했던 분류 모형 처럼 이번에는 1990년 캘리포니아 인구 조사의 정보 데이터를 가지고 주택 가격(median House Value)를 예측하는 회귀 모형을 작성한 것을 리뷰한다.

 

housing_data(회귀) (1).csv
0.96MB

 

다음은 housing_data(회귀).csv 데이터를 분석에 적합한 형태로 준비하기 위해 수행한 전처리 과정을 정리한 내용이다. 이 전처리 과정을 통해 데이터의 품질을 개선하고, 모델이 안정적으로 학습할 수 있는 환경을 조성하였다.

1. 전처리

 우선 데이터셋의 각 열에 결측치가 있는지 확인하였다. 결측치는 회귀 모델의 계산을 중단시키거나, 모델 성능을 저하시킬 수 있기 때문에 사전에 처리해야 한다.

 

 결측치가 발견된 수치형 변수(예: total_bedrooms)에 대해 중위수(median)를 사용하여 대체하였다. 중위수를 사용한 이유는 다음과 같다.

  • 비대칭 분포에 적합: 예를 들어, median_income 변수는 오른쪽 꼬리가 긴 비대칭 분포를 나타냈다. 이 경우, 평균은 극단값의 영향을 받아 데이터의 중심을 제대로 반영하지 못할 수 있으나, 중위수는 데이터의 중심 경향을 안정적으로 나타낼 수 있다.
  • 이상치의 영향 최소화: 중위수는 이상치의 영향을 받지 않아 데이터의 왜곡을 최소화한다.

비대칭을 확인하기 위해 왜도 값을 기반으로 시각화를 해보겠다. 왜도 값이 0에 가까울수록 대칭적이고, 0에서 멀어질수록 비대칭임을 나타낸다.

비대칭이 심각한 특성들이 보인다。

 

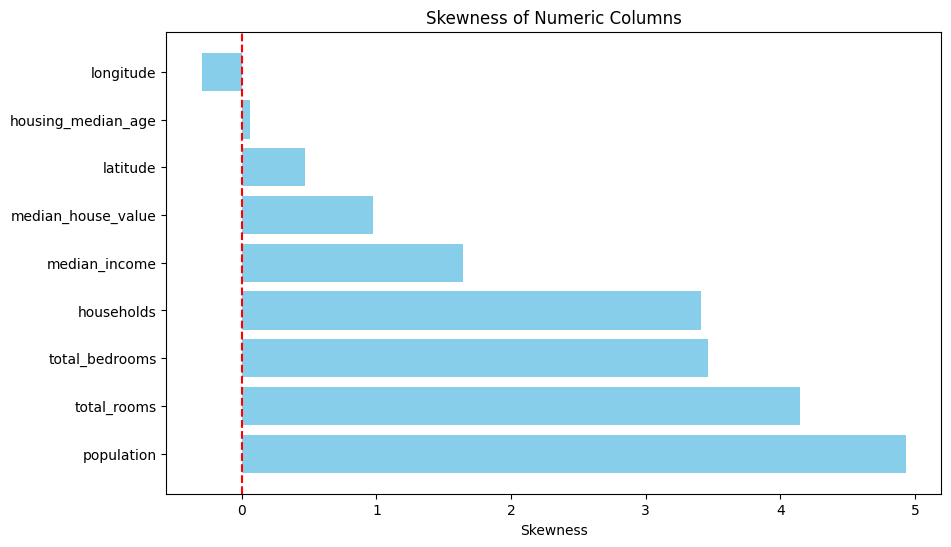
 비대칭으로 인한 극단값에 영향을 최소화 하기위해 total_bedrooms 변수에서 207개의 결측치를 중위수로 대체하였다.

 


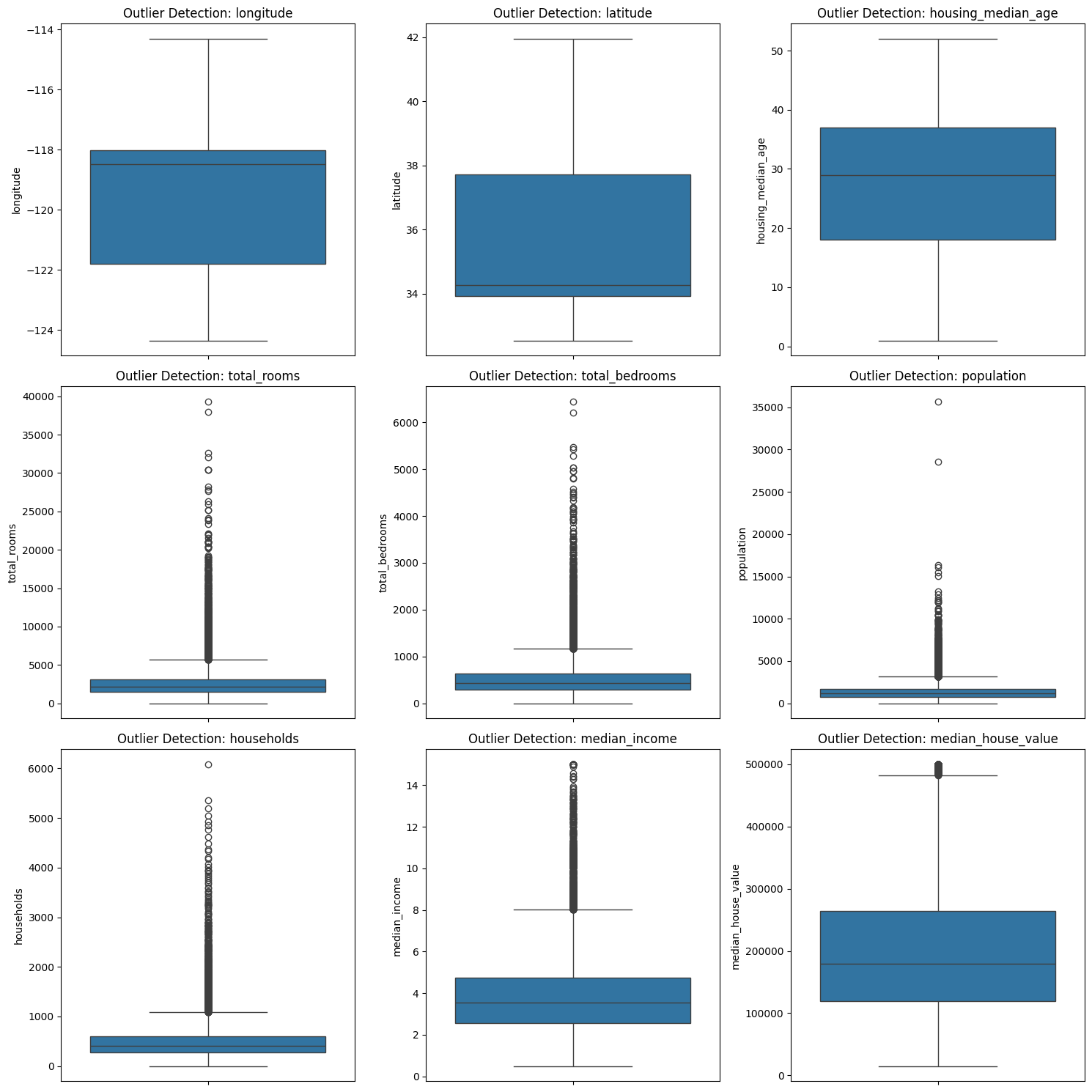
 또한 이상치를 탐지하기 위해 상자 그림(Box Plot)을 사용하여 각 수치형 변수의 분포를 시각적으로 확인하였다.
IQR(Interquartile Range) 방식을 활용하여, 1사분위(Q1)와 3사분위(Q3)의 범위를 벗어난 값을 이상치로 간주하였다.


이상치로 판별된 값은 해당 변수의 중위수로 대체하였다( 이때 평균으로 대체 한걸 끝나고 발견해서 전부 새로해야했음..). 수치형 변수에 대해 표준화를 진행하였다. 표준화는 데이터의 평균을 0, 표준편차를 1로 맞추는 과정으로, 변수 간의 스케일 차이를 줄이는 데 유용하다.

  • 모델 성능 개선: 회귀 모델이나 거리 기반 모델은 변수 크기에 민감하다. 표준화를 통해 이러한 민감성을 제거하고, 모델이 변수 간의 상대적인 관계에 집중하도록 하였다.
  • 단위 차이 제거: 다양한 단위로 구성된 데이터를 표준화함으로써, 모델이 특정 변수의 크기 차이에 의해 편향되지 않도록 하였다.

본 데이터셋에는 범주형 변수가 존재하지 않았으므로, 별도의 인코딩 과정을 수행하지 않았다. 범주형 변수가 없는 경우, 인코딩은 불필요하며, 이를 통해 전처리 과정을 간소화하였다.

 

이번 전처리 과정에서는 결측치 처리, 이상치 처리, 표준화 등의 전처리 과정을 수행하였다. 이 전처리 과정을 통해 데이터의 노이즈를 최소화하고, 모델이 안정적으로 학습할 수 있는 환경을 마련하였다. 결과적으로, 모델이 데이터의 핵심 패턴을 효과적으로 학습하고, 높은 일반화 성능을 달성할 수 있도록 준비하였다.

 

2. 회귀 모형

다중 회귀모형을 통해 예측한 모델의 성능 평가는 다음과 같다.

# 필요한 라이브러리 임포트
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score, mean_absolute_error  # MAE 추가
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

# 데이터 분리 및 스케일링
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# 모델 학습
model = LinearRegression()
model.fit(X_train_scaled, y_train)

# 예측
y_pred = model.predict(X_test_scaled)

# 모델 평가
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
r2 = r2_score(y_test, y_pred)
n = X_test.shape[0]
p = X_test.shape[1]
adjusted_r2 = 1 - (1 - r2) * (n - 1) / (n - p - 1)

print("모델 성능 평가:")
print(f"RMSE: {rmse}")
print(f"R²: {r2}")
print(f"Adjusted R²: {adjusted_r2}")

# MAE 추가
mae = mean_absolute_error(y_test, y_pred)
print(f"MAE: {mae}")

# 잔차 분석
residuals = y_test - y_pred
plt.scatter(y_pred, residuals)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel("Predicted Values")
plt.ylabel("Residuals")
plt.title("Residual Analysis")
plt.show()

 

  • RMSE (Root Mean Squared Error): 0.723
    예측값과 실제값 사이의 평균적인 오차를 나타낸다. 값이 낮을수록 모델의 예측이 정확하다.
  • R² (결정계수): 0.482
    독립 변수가 종속 변수의 변동을 48.2% 설명하고 있음을 의미한다. 이 값은 독립 변수가 추가될수록 증가할 수 있어, 설명력이 충분히 높다고 보기 어렵다. -> 조정된 결정 계수 보기
  • Adjusted R² (조정된 결정계수): 0.481
    R² 값을 독립 변수의 개수를 고려하여 보정한 지표로, 모델이 유의미한 변수만 포함했는지 평가하는 데 유용하다. 독립 변수의 개수를 고려했을 때도 설명력이 비슷한 수준임을 보여준다.
  • MAE (Mean Absolute Error): 0.531
    예측값과 실제값의 절대 오차 평균으로, 데이터의 오차를 직관적으로 파악할 수 있다.

RMSE와 MAE를 비교했을 때, 모델의 오차가 대부분 0.723 이내이며, 절대적인 평균 오차도 0.531로 비교적 안정적이다. 그러나 R²와 조정된 R²가 0.5 미만으로, 독립 변수가 종속 변수의 변동을 절반 정도만 설명하고 있다. -> 잘 설명 못함

 

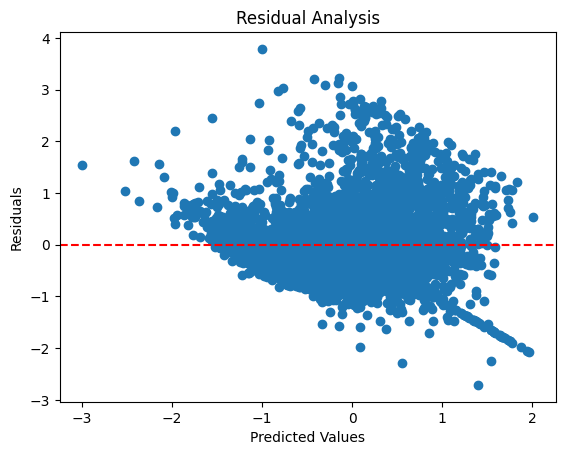
 잔차 그래프도 예측값과 잔차 간 분포가 무작위로 보이며 특정구간에서 잔차가 커지는 패턴이 관찰된다. 이는 일부 모델에서 과소 또는 과대 예측을 하고 있을 수 있다. 

 

3. KNN

# 필요한 라이브러리 불러오기
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.preprocessing import StandardScaler

# KNN 모델 학습 (기본 k=5 사용)
knn = KNeighborsRegressor(n_neighbors=5)
knn.fit(X_train, y_train)

# 예측
y_pred = knn.predict(X_test)

# 모델 성능 평가
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
r2 = r2_score(y_test, y_pred)
adjusted_r2 = 1 - (1 - r2) * (n - 1) / (n - p - 1)

print("KNN 기본 모델 성능 평가:")
print(f"RMSE: {rmse}")
print(f"R²: {r2}")
print(f"Adjusted R²: {adjusted_r2:.3f}")

'''KNN 기본 모델 성능 평가:
RMSE: 0.6833766267742908
R²: 0.5373014244025884
Adjusted R²: 0.536'''

 

기본 설정으로 k=5를 사용하여 KNN 모델을 학습한 결과.

  • RMSE: 0.683
    예측값과 실제값의 평균적인 오차를 나타냄.
  • R²: 0.537
    독립 변수가 종속 변수의 약 53.7%를 설명.
  • Adjusted R²: 0.536
    조정된 결정계수는 모델 복잡성을 고려했을 때 설명력이 크게 달라지지 않았음을 보여줌.

하이퍼 파라미터 튜닝은 다음과 같음.

from sklearn.decomposition import PCA
from sklearn.neighbors import KNeighborsRegressor
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer, mean_squared_error

# 파이프라인 구성: PCA + KNN
pipeline = Pipeline([
    ('pca', PCA()),  # PCA 단계
    ('knn', KNeighborsRegressor())  # KNN 단계
])

# 하이퍼파라미터 그리드 정의 (n_components 범위 조정)
param_grid = {
    'pca__n_components': [1, 2, 3, 4, 5, 6, 7, 8],  # PCA 차원 수 조정
    'knn__n_neighbors': [3, 5, 7, 9, 11, 13],  # K의 값
    'knn__weights': ['uniform', 'distance'],  # KNN 가중치
    'knn__metric': ['euclidean', 'manhattan']  # 거리 척도
}

# GridSearchCV 설정 (RMSE 기준으로 최적화)
scorer = make_scorer(mean_squared_error, greater_is_better=False)  # MSE를 음수로 설정하여 최적화
grid_search = GridSearchCV(estimator=pipeline, param_grid=param_grid, scoring=scorer, cv=5)

# 학습 및 최적의 하이퍼파라미터 찾기
grid_search.fit(X_train, y_train)

# 최적의 하이퍼파라미터와 점수 확인
print("Best parameters:", grid_search.best_params_)
print("Best RMSE:", np.sqrt(-grid_search.best_score_))

'''Best parameters: {'knn__metric': 'manhattan', 'knn__n_neighbors': 13, 'knn__weights': 'distance', 'pca__n_components': 8}
Best RMSE: 0.6426464113808621'''

 

모델 성능 향상을 위해 다음과 같은 두 가지 방법을 적용하였다.

  1. PCA(주성분 분석):
    • 데이터 차원을 줄여 계산 효율성을 높이고, 모델 학습 시 불필요한 변수를 제거.
  2. 하이퍼파라미터 튜닝:
    • k(이웃 수), 거리 척도(metric), 가중치 방식(weights), PCA 차원 수(n_components)를 조정.

최적화된 하이퍼파라미터:

  • PCA 차원 수: 8
  • 이웃 수 (k): 13
  • 가중치 (weights): distance
  • 거리 척도 (metric): manhattan

이 설정을 통해 최적의 모델을 학습하였으며, 5-Fold 교차 검증을 통해 최적화된 RMSE를 도출했습니다.

  • Best RMSE: 0.643
    최적화된 모델의 교차 검증 평균 RMSE 값.

이제 이후에 최적화된 파라미터 값으로 재 훈련한 모델 성능은

 

  • RMSE: 0.649 - 예측값과 실제값 간 평균적인 오차로, 기본 모델에 비해 5%가량 감소.
  • R²: 0.583 - 기본 모델 대비 향상.
  • Adjusted R²: 0.582

실제 값과 예측값의 관계를 보여주는 잔차 분석을 실시함. 빨간색 점선은 예측값과 실제값이 완전히 일치할 경우의 이상적인 선형 관계를 보여준다.

 

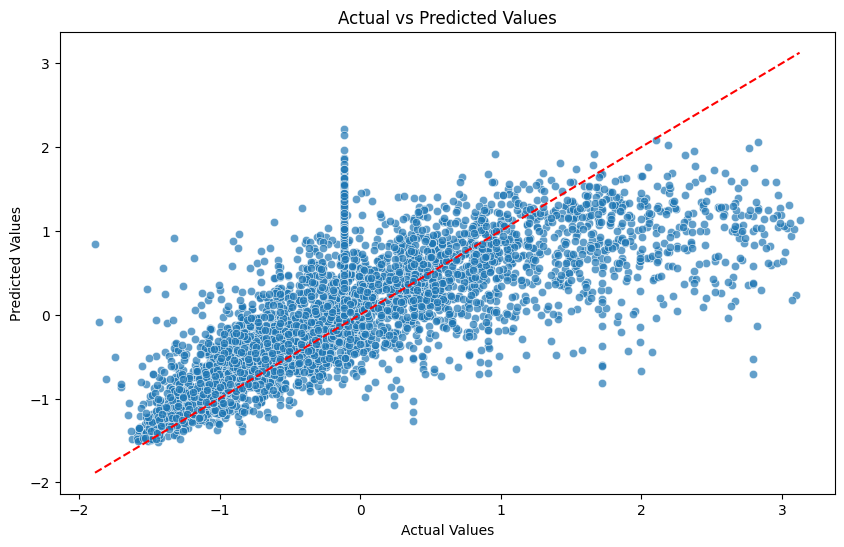
 다는 아니지만, 어느정도 선형성을 확인 할 수있다. 모델이 데이터의 전반적인 패턴을 학습했지만, 특정 데이터 구간에서는 선형성이 약화된 것으로 보인다. 오차 분포는 특정 구간 - 0 부분에서 밀집된 점 - 에서 잔차의 증가가 보이며 (검토 필요) 해당 부분에서 학습이 올바르지 못했을 수 있음. 그래프에서 약간의 비대칭성이 나타나는 구간이 있어 모델이 데이터의 특정 비선형 관계를 충분히 학습하지 못했을 가능성이 있음.

 

'머신러닝' 카테고리의 다른 글

파이썬과 케라스를 이용한 간단한 딥러닝 +  (1) 2024.11.28
지도학습 - 대출 승인 결과 분류 예측모형 / 앙상블  (1) 2024.11.23
지도학습 - 대출 승인 결과 분류 예측모형 / Tree,SVM  (0) 2024.11.14
지도학습 - 대출 승인 결과 분류 예측모형 / 전처리, 로지스틱 회귀모형, KNN  (0) 2024.11.13

관련글

티스토리툴바